Мастерим Математику: Как Понять Достаточные Условия Возрастания и Убывания Функции

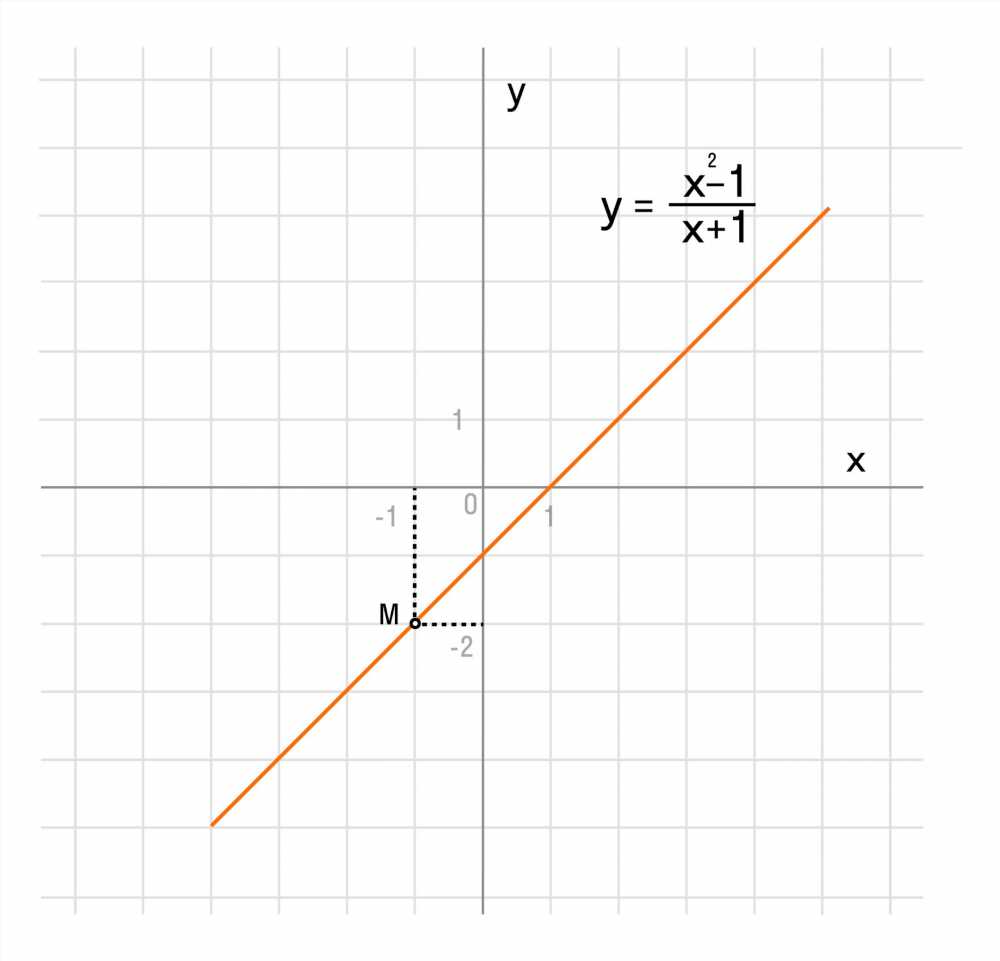
В мире математики, особенно в алгебре и анализе, понимание условий возрастания и убывания функций играет ключевую роль. Это не только помогает в построении графиков функций, но и в определении экстремумов и поведения функций в различных точках. В этой статье мы рассмотрим, что такое достаточные условия возрастания и убывания функции, и как они применяются в математике.

Что такое достаточные условия возрастания и убывания функции?

Достаточные условия возрастания и убывания функции - это критерии, которые позволяют определить, когда функция возрастает или убывает в заданной точке или на интервале. Эти условия играют важную роль в анализе поведения функций и помогают нам делать выводы о характере изменения функции.

Достаточные условия возрастания функции

1. Производная функции

Одним из основных инструментов для определения условий возрастания функции является её производная. Если производная функции положительна на каком-либо интервале, то функция возрастает на этом интервале.

2. Вторая производная функции

Для более точного определения условий возрастания функции, можно использовать вторую производную. Если вторая производная положительна на интервале, то это говорит о том, что функция выпукла вверх и, следовательно, возрастает.

3. Исследование точек экстремума

При анализе условий возрастания функции также важно изучать точки экстремума. Если функция имеет локальный минимум в некоторой точке, то в её окрестности она будет возрастать.

Достаточные условия убывания функции

1. Производная функции

Аналогично условиям возрастания, производная функции играет ключевую роль в определении убывания. Если производная функции отрицательна на интервале, то функция убывает на этом интервале.

2. Вторая производная функции

Вторая производная также может использоваться для анализа убывания функции. Если она отрицательна на интервале, то функция выпукла вниз и, следовательно, убывает.

3. Исследование точек экстремума

Точки экстремума также играют важную роль при анализе условий убывания функции. Если функция имеет локальный максимум в некоторой точке, то в её окрестности она будет убывать.

Заключение

Достаточные условия возрастания и убывания функции предоставляют нам мощный инструмент для анализа поведения функций на интервалах. Понимание этих условий помогает нам строить графики функций, находить экстремумы и делать выводы о характере изменения функции в различных точках. Это основа для более глубокого изучения математики и её применения в различных областях науки и инженерии.